transforms

2D Matrix transformations to manipulate a series of (x,y) coordinates.

2D Affine Transformations

For manipulating sets of stroke-3 coordinates, I often needed to transform the coordinates - rescaling, rotating, moving, etc.

2D affine transformations are perfect for this. Each transformation is expressed as a matrix, and is applied by performing matrix multiplication against the 2D matrix of coordinates (with a column of 1 values concatenated next to x and y values).

def apply_transform(coords_2d, xform):
    assert coords_2d.shape[1] == 2
    assert xform.shape[0] == 3
    assert xform.shape[1] == 3

    coords_full = np.concatenate([coords_2d, np.ones((coords_2d.shape[0], 1))], axis=1)
    assert coords_full.shape[0] == coords_2d.shape[0]
    assert coords_full.shape[1] == 3

    return xform.dot(coords_full.transpose()).transpose()[:,:2]

apply_transform

 apply_transform (coords_2d, xform)

Consider a sample set of x,y coordinates:

x	y
0	0
0.5	0.5
1	1

The simplest affine transformation is the identity.

Multiplying the 2D coords by the following matrix will output an identical set of coordinates:

1   0   0
0   1   0
0   0   1

def identity_xform():
    return np.array([
        [1, 0, 0],
        [0, 1, 0],
        [0, 0, 1]])

identity_xform

 identity_xform ()

sample_coords = np.array([
    [0.0,0.0],
    [0.5,0.5],
    [1.0,1.0],
])

test(apply_transform(sample_coords, identity_xform()),
     sample_coords,
     np.array_equal)

Scaling a set of coordinates by sx in the x direction and sy in the y direction is as easy as multiplying by:

sx  0   0
0   sy  0
0   0   1

def scale_xform(sx, sy):
    return np.array([
        [sx, 0, 0],
        [0, sy, 0],
        [0, 0, 1]])

scale_xform

 scale_xform (sx, sy)

scaled_coords_2x_3y = np.array([
    [0.0,0.0],
    [1.0,1.5],
    [2.0,3.0],
])

test(apply_transform(sample_coords, scale_xform(sx=2.0, sy=3.0)),
     scaled_coords_2x_3y,
     np.array_equal)

Translating a set of coordinates by tx in the x direction and ty in the y direction uses the following matrix.

1   0   tx
0   1   ty
0   0   1

def translate_xform(tx, ty):
    return np.array([
        [1, 0, tx],
        [0, 1, ty],
        [0, 0, 1]])

translate_xform

 translate_xform (tx, ty)

translated_coords_2x_3y = np.array([
    [2.0,3.0],
    [2.5,3.5],
    [3.0,4.0],
])

test(apply_transform(sample_coords, translate_xform(tx=2.0, ty=3.0)),
     translated_coords_2x_3y,
     np.array_equal)

To rotate a set of 2D coordinates by n degrees, we first convert the desired angle of rotation from degrees to a value in radians, theta.

Consider a point (x1, y1) at (4, 4) that I want to rotate by 30 degrees around the origin. If I make a line to the origin with length r, the angle between line1 and the x axis, which I’ll call phi, is 45 degrees.

x1 = r * cos(phi) = 4
y1 = r * sin(phi) = 4

If I want to rotate it by 30 degrees, its final position at point (x2, y2) will be 45 + 30 = 75 degrees from the x-axis, equivalent to phi + theta.

x2 = r * cos(phi + theta)
y2 = r * sin(phi + theta)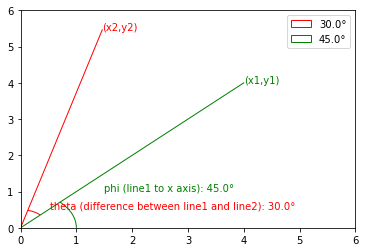

Since cos(a + b) = cos(a)*cos(b) - sin(a)*sin(b) and sin(a + b) = sin(a)*cos(b) + cos(a)*sin(b), this breaks down into:

x2 = r * cos(phi + theta)
   = r * cos(phi) * cos(theta) - r * sin(phi) * sin(theta)
   = x1 * cos(theta) - y1 * sin(theta)

y2 = r * sin(phi + theta)
   = r * sin(phi) * cos(theta) + r * cos(phi) * sin(theta)
   = y1 * cos(theta) + x1 * sin(theta)

So, multiplying any 2D coordinates by the following matrix will produce the correct rotation:

cos(theta)   -sin(theta)  0
sin(theta)   cos(theta)   0
0            0            1

def rotate_xform(rotate_angle):
    if rotate_angle % 360 == 0:
        return identity_xform()
    theta = np.radians(rotate_angle)
    cos_theta = np.cos(theta)
    sin_theta = np.sin(theta)
    return np.array([
        [cos_theta, -sin_theta, 0],
        [sin_theta, cos_theta, 0],
        [0, 0, 1]
    ])

rotate_xform

 rotate_xform (rotate_angle)

Bounding Boxes

class BoundingBox:
    xmin: float
    xmax: float
    ymin: float
    ymax: float
    xrange: float
    yrange: float

    def __init__(self, xmin, xmax, ymin, ymax):
        assert xmin <= xmax
        assert ymin <= ymax
        self.xmin = xmin
        self.xmax = xmax
        self.ymin = ymin
        self.ymax = ymax
        self.xrange = xmax - xmin
        self.yrange = ymax - ymin

    def __repr__(self):
        return f"BBox(({self.xmin}, {self.ymin}), ({self.xmax}, {self.ymax})) (width {self.xrange} x height {self.yrange})"

    @staticmethod
    def create(coords: np.ndarray):
        # rank-2
        if len(coords.shape) == 2:
            xmin = coords[:, 0].min()
            xmax = coords[:, 0].max()

            ymin = coords[:, 1].min()
            ymax = coords[:, 1].max()

            return BoundingBox(
                xmin=xmin, xmax=xmax, ymin=ymin, ymax=ymax
            )
        else:
            raise Exception(f"invalid coordinates passed - expected rank-2 matrix but got rank-{len(coords.shape)}")

    def merge(self, other):
        return BoundingBox(
            xmin=min(self.xmin, other.xmin),
            xmax=max(self.xmax, other.xmax),
            ymin=min(self.ymin, other.ymin),
            ymax=max(self.ymax, other.ymax),
        )

    def area(self):
        return self.xrange * self.yrange

    def intersection(self, other):
        bb1 = self
        bb2 = other

        assert bb1.xmin <= bb1.xmax
        assert bb1.ymin <= bb1.ymax
        assert bb2.xmin <= bb2.xmax
        assert bb2.ymin <= bb2.ymax

        x_left = max(bb1.xmin, bb2.xmin)
        y_top = max(bb1.ymin, bb2.ymin)
        x_right = min(bb1.xmax, bb2.xmax)
        y_bottom = min(bb1.ymax, bb2.ymax)

        if x_right < x_left or y_bottom < y_top:
            return None
        
        return BoundingBox(xmin=x_left, ymin=y_top, xmax=x_right, ymax=y_bottom)

    def iou(self, other):
        """
        Intersection over union - area of the overlap relative to combined area of the bounding boxes
        """
        overlap = self.intersection(other)
        if not overlap:
            return 0.0
        return overlap.area() / float(self.area() + other.area() - overlap.area())
        
    def normalization_xform(self, scale=1.0):
        """
        Produce a normalization transform - a set of transformations,
        given the input coordinates, to convert all coords into the range (0,1)
        """
        max_range = self.xrange if self.xrange > self.yrange else self.yrange
        return scale_xform(scale / max_range, scale / max_range).dot(
            translate_xform(-self.xmin, -self.ymin)
        )

BoundingBox

 BoundingBox (xmin, xmax, ymin, ymax)

Initialize self. See help(type(self)) for accurate signature.

BoundingBox.create

 BoundingBox.create (coords:numpy.ndarray)

BoundingBox.merge

 BoundingBox.merge (other)

BoundingBox.area

 BoundingBox.area ()

BoundingBox.intersection

 BoundingBox.intersection (other)

BoundingBox.iou

 BoundingBox.iou (other)

Intersection over union - area of the overlap relative to combined area of the bounding boxes

BoundingBox.normalization_xform

 BoundingBox.normalization_xform (scale=1.0)

Produce a normalization transform - a set of transformations, given the input coordinates, to convert all coords into the range (0,1)

Stroke-3 Conversion

strokes_to_deltas

 strokes_to_deltas (strokes)

points_to_deltas

 points_to_deltas (points)

strokes_to_points

 strokes_to_points (strokes)

deltas_to_strokes

 deltas_to_strokes (_seq)

points_to_strokes

 points_to_strokes (_seq)

deltas_to_points

 deltas_to_points (_seq)

RDP

rdp_strokes

 rdp_strokes (strokes, epsilon=1.0)

stroke_rdp_deltas

 stroke_rdp_deltas (rescaled_strokes, epsilon=2.0)